Graph Representations: A Comprehensive Guide

In this post, we will look at various graph representations and how to translate the representation to the code in Java.

Graph Representation

In order to represent a graph in code, you have to store information about

1. The Vertices which are part of the given Graph and,
2. The Edges which connect vertices

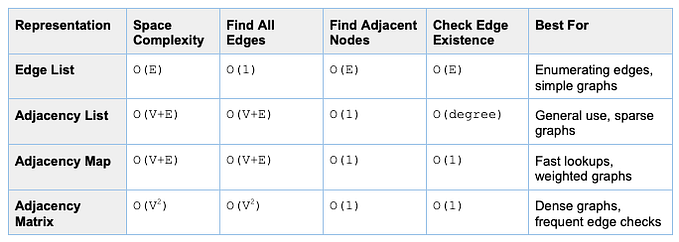
Graphs can be represented in various ways in programming. The most common representations are: Adjacency Matrix, Adjacency List and Edge List

Adjacency Matrix Representation of Graphs

An adjacency matrix is a 2D array used to represent a graph. In this representation, the graph is described by a square matrix A of size V x V where V is the number of vertices. Each element A[i][j] indicates whether there is an edge from vertex i to vertex j.

Characteristics

• Storage: Uses O(V2) space, where V is the number of vertices.
• Edge Presence: A[i][j] = 1 if there is an edge from vertex i to vertex j, otherwise A[i][j] = 0.
• Weighted Graphs: For weighted graphs, A[i][j] can store the weight of the edge.
• Use Case: Efficient for dense graphs where the number of edges E is close to V2, and for quickly checking the presence of edges.

Example

Consider a simple undirected graph with 4 vertices (0, 1, 2, 3) and 4 edges:

Adjacency Matrix Representation

The adjacency matrix for this graph would be:

Java Implementation

Here’s how you can represent and print an adjacency matrix in Java:

// Class to represent a graph using adjacency matrix
class Graph {
    private final int[][] adjMatrix;
    private final int V;

    // Constructor
    public Graph(int V) {
        this.V = V;
        adjMatrix = new int[V][V];
    }

    // Method to add an edge to the graph
    public void addEdge(int src, int dest) {…